汎純正律のつかいかた⓪
20250613
目次
- 1. 汎純正律と音程空間の構造
- 1-1. 音律と次元
- 1-2. 汎純正律の定義と構造
- 2. 汎純正律の旋律
- 2-1. 比率系的な旋律
- 2-2. 既存純正律体系の包含
- 3. 汎純正律の和音
- 3-1. Order-kとn-limit
- 3-2. 従来的コード進行とその記述例
- 4. まとめと今後の展望
1. 汎純正律と音程空間の構造
1-1. 音律と次元
音楽は「音の高さの関係」で成り立っている。そして音律とは、それら高さの関係を系統的に構成・定義するルールである。
$$
\def\arraystretch{1.5}
\begin{array}{|c|c|c|}\hline
音律 & 素因数基底 & 自由度と形状 \\ \hline
ピタゴラス& \{2,3\} & 2\mathrm{D}格子 \\
\hdashline
5\mathrm{-limit}純正律 & \{2,3,5\} & 3\mathrm{D}格子 \\
\hdashline
7\mathrm{-limit}純正律 & \{2,3,5,7\} & 4\mathrm{D}格子 \\
\hdashline
11\mathrm{-limit}純正律 & \{2,3,5,7,11\} & 5\mathrm{D}格子 \\
\hdashline
12平均律 & – ^{※1}& 1\mathrm{D}環状格子 \\ \hdashline
中全音律 & \{2,3,5\}\:(+\mathrm{temper}) & 1\mathrm{D}折り畳み ^{※2}\\
\hdashline
\mathrm{JT\;Bohlen–Pierce}^{※3} & \{3,5,7\} & 3\mathrm{D}格子 \\ \hdashline
汎純正律 & \mathbb{P} & ∞次元格子^{※4} \\
\hline
\end{array}
$$
※1: 12平均律は \({2^{1/12}}\) を唯一の生成元とし、整数比をすべて等分化しているため固有の素因数基底を持たない(が、アプローチは5-limit的)
※2: 2D格子を巻き取った1D sub-lattice
※3: Just Tuned Bohlen-Pierce (3, 5, 7 limit)
※4: \({\displaystyle \bigoplus_{p\in\mathbb{P}} \mathbb{Z}}\)
ここで導入される汎純正律は∞-limitな純正律構文の拡張であり、全ての有理数比を任意に、誤差なく、任意の実数比をε精度で近似できるほど稠密にして使用可能な原理上最も包摂的な音律である。
以下、演奏はこれを想定するものとし、操作方法も以下の通りである:

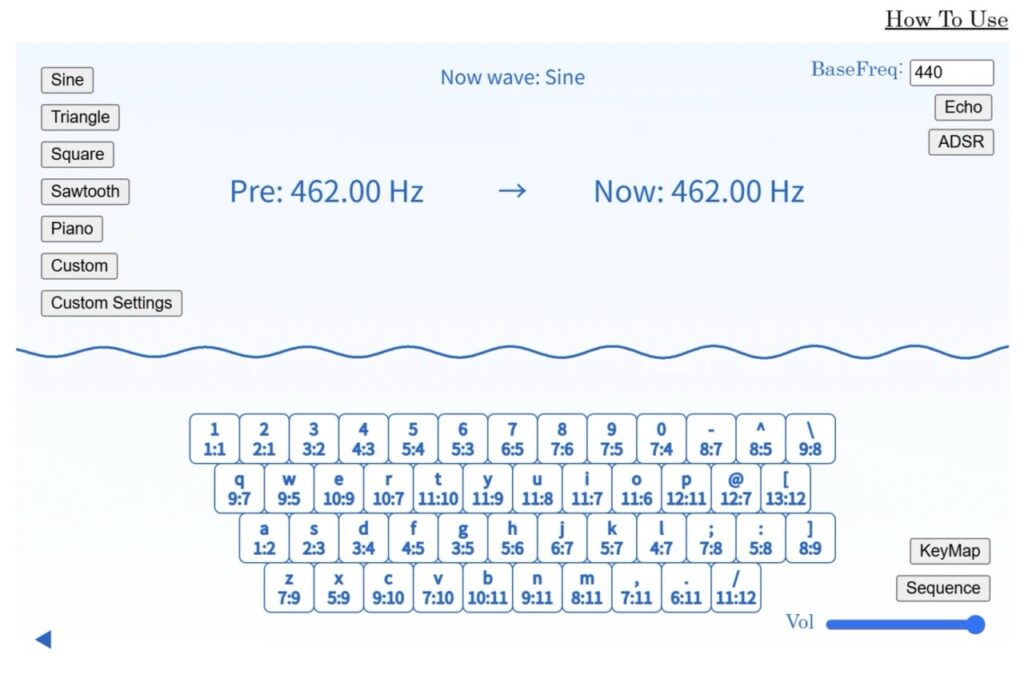
キャンバス表示後、Enterもしくは画面クリック/タップにより440Hzの開始音が鳴り、入力及び動作が開始します。
・音色変更ボタン(画面左):音色をsine, triangle, square, sawtooth, piano, customから選択できます。そのうち音色Customは下方のCustom Settingsにより倍音ごとに波形を合成可能です。
・Now Wave表示(画面中央上):現在の音色を表示します。
・Pre, Now表示:比率の入力をし音を鳴らした時、比率が掛けられる前の周波数をPreに、掛けられた後現在鳴っている周波数をNowに表示します。
・キーボードボタン(中央下):キーボードの押下または対応する位置をクリック/タップすることで比率を入力します。
・Basefreq Input(右側最上):Now frequencyを直入力により変更します。
・Echoボタン(右側上中):Echoパネルを開きます。EchoパネルではReverbとDelayの数値を変更できます。どの音色にも有効です。
・ADSRボタン(右側上下):ADSRパネルを開きます。ADSRパネルではAttack, Decay, Sustain, Releaseスライダーを用いた音色の生成とその有効/無効化の設定ができます。Piano以外の音色に有効です。
・Volスライダー(右側最下):Volumeを変更します。どの音色にも有効です。
・KeyMapボタン(右側下上):KeyMapパネルを開きます。KeyMapパネルでは各キーボードボタンの配置と比率を変更することができます。
・Sequenceボタン(右側下中央):Sequenceパネルを開きます。Sequenceパネルでは演奏データの保存・編集・再生などが可能です。
1-2. 汎純正律の定義と構造
汎純正律(Pan-Just Intonation, PJI または Ratio Tuning)に於いて、すべての音は直前の音との周波数比によって定義され、音高列 \({\{f_0, f_1, f_2, \ldots\}}\) は以下のように表される。
・\({f_0}\):初期音
・\({r_n}\):第 \(n\) 音から第 \(n+1\) 音への比率(演奏者または作曲者が逐次選択)
・\({\mathbb{Q}^{+}}\):正の有理数
特定の中心音(トニック)や固定音階を持たず、演奏開始点およびその後の比率の列に応じて音列が定まる。また使用される比は任意の正の有理数でよく、2:3 や 5:4、17:16 など、理論上すべて選択可能である。
連続的に比をとるため、任意の2音間の比率は以下の式で表される:
$$
\mathrm{Interval}(i,j)=\frac{f_j}{f_i}=\prod_{k=i}^{j-1}r_k
$$
汎純正律は ∞-limitな純正律構文の拡張と見なせるが、当音律が目的としているのは単に「多くの音程を許す」ことだけではなく、従来の音律にみられるような固定音を廃し、比率とその系列自体を音楽の主体とするという構造的転換でもある。そういった意味では \({\displaystyle\lim_{n\to \infty} n\mathrm{-limit}}\) ではないとも言える。
Sequence Inputに以下を入力してみよう:
100ms, prefreq=490
800ms, 3:4, 3500ms
1700ms, 11:7, 3500ms
5拍, 10:9, 3000ms
3400ms, 3:2, 2500ms
msによる入力と拍による入力が可能
以上のInputは \({f_0=490 \;\mathrm{Hz}}\) として、順に比率列 \({\mathbf{r}=\left\{\frac{3}{4}, \frac{11}{7}, \frac{10}{9}, \frac{3}{2}\right\} }\) に従った4音を生成するSequenceである。
$$
\def\arraystretch{1.5}
\begin{array}{|c|c|c|}\hline
比率 & 素因数 & 比率の調和名 \\ \hline
\frac{3}{4} & 2^{-2}\cdot 3 & \mathrm{(invert)\:perfect \:fourth} \\
\hdashline
\frac{11}{7} & 7^{-1}\cdot 11 & \mathrm{undecimal \:augmented \:fifth} \\
\hdashline
\frac{10}{9} & 2\cdot 3^{-2}\cdot 5 & \mathrm{minor\: whole \:tone} \\
\hdashline
\frac{3}{2} & 2\cdot 3 & \mathrm{perfect \:fifth} \\
\hline
\end{array}
$$
2. 汎純正律の旋律
2-1. 比率系的な旋律
汎純正律では音高の絶対値・比率列の初期値は重要視されず、比率の重複で旋律が発生する。そのため旋律や和音の分析をするにあたって重要視されるのは構成音ではなく比率とその経路である。
この場合多くは絶対音高や調的中心をもたず、やや安定感のない(あるいは予測しにくい)旋律が発生させられることになる。比率を低limitに限定しても、響き自体は安定するが旋律はやはり気まぐれなものになる。その中でつかみどころのある”旋律的”な印象を与えるための技法として、繰り返しは依然有効な手立てであるといえるだろう。また2-2で後述するように、比率的でない、既存の音楽理論に近い調などを用いたアプローチも完全なかたちで利用可能である。
1000ms, 3:2, 1200ms
1300ms, 7:5, 1200ms
1600ms, 5:8, 1200ms
2200ms, 3:2, 1200ms
2500ms, 7:5, 1200ms
2800ms, 5:8, 1200ms
反復
周期内での比率の累積が1になるようにして、より完全なループを作ることもできる。
1000ms, 3:4, 1200ms
1300ms, 2:1, 1200ms
1600ms, 2:3, 1200ms
2200ms, 3:4, 1200ms
2500ms, 2:1, 1200ms
2800ms, 2:3, 1200ms
完全反復
繰り返しではないが、以下のような構成も乱雑な比率列より安定感のある旋律を持つ。
1000ms, 3:5, 1200ms
1300ms, 10:7, 1200ms
1600ms, 10:7, 1200ms
1900ms, 3:5, 1200ms
回文
1000ms, 8:5, 1200ms
1300ms, 5:7, 1200ms
1600ms, 7:6, 1200ms
1900ms, 6:11, 1200ms
連鎖
特に連鎖型の旋律は、2ステップ以上前の音から見た累積比も単純な数値になる為、安定した響きを得られると考えられる。
2-2. 既存純正律体系の包含
また、事前に用意した比率プリセット中の比率だけで音高列を生成していくことによって、従来の音楽理論のスケール等を利用することもできる。たとえばピタゴラス音律であれば音律を構成する比率は一度を含めて13個存在しているので、その直積集合をとれば汎純正律内でピタゴラス音律を完全に実現するだけのプリセットが完成することになる。このような機能は汎純正律のうちの∞-limit的な機能である(比率主軸と対比して)。
$$
\mathbf{r}_{\mathrm{Pyt}}=\left\{\frac{1}{1}, \frac{4}{3},\frac{3}{2},\ldots,\frac{1024}{729}\right\}
$$
$$
\mathbf{r}_{\mathrm{PJI-Pyt}}=\mathbf{r}_{\mathrm{Pyt}}^2
$$
100ms, prefreq=440
700ms, 1:1, 1200ms
1000ms, 9:8, 1200ms
1300ms, 9:8, 1200ms
1600ms, 256:243, 1200ms
1900ms, 9:8, 1200ms
2200ms, 9:8, 1200ms
2500ms, 9:8, 1200ms
2800ms, 256:243, 1200ms
ピタゴラス音律のCメジャースケール
もちろん美的追求のためにスケールが既存である必要は皆無である。
3. 汎純正律の和音
3-1. Order-kとn-limit
便宜上、汎純正律の中の所定の部分を以下のように呼称することにする。
$$
\def\arraystretch{1.5}
\begin{array}{|c|c|c|c|c|}\hline
名称 & 素因数 & 例 & 体感 \\ \hline
\mathrm{Order-1} & 5\mathrm{-limit}以下純正比 & 1,\frac{5}{4},\frac{3}{2} & 安定 \\
\hdashline
\mathrm{Order-2} & 7〜11\mathrm{-limit}純正比 & \frac{7}{4},\frac{11}{8} & 曖昧, 浮遊感 \\
\hdashline
\mathrm{Order-3} & 13以上\mathrm{-limit}純正比 & \frac{13}{8},\frac{19}{17} & 金属的, 緊迫(?)\\
\hline
\end{array}
$$
比率は 低Order→高Order→低Order のかたちで配置すると機能的な緊張・弛緩が生まれる。
100ms, prefreq=500
700ms, 1:1, 1200ms
1000ms, 5:4, 900ms
1300ms, 6:5, 600ms
2000ms, prefreq=500
2600ms, 1:1, 1200ms
2600ms, 5:4, 1200ms
2600ms, 6:5, 1200ms
Order-1での和音例(Iメジャー)
100ms, prefreq=100
700ms, 8:3, 1200ms
1000ms, 8:3, 900ms
1300ms, 8:3, 600ms
2000ms, prefreq=100
2600ms, 8:3, 1200ms
2600ms, 8:3, 1200ms
2600ms, 8:3, 1200ms
11度堆積
100ms, prefreq=300
700ms, 2:3, 1200ms
1000ms, 7:3, 900ms
1300ms, 19:17, 600ms
2000ms, prefreq=300
2600ms, 2:3, 1200ms
2600ms, 7:3, 1200ms
2600ms, 19:17, 1200ms
perfect fifth, minimal tenth, quasi-meantone
3-2. 従来的コード進行とその記述例
和音を並べるにあたって、最低音を前回の和音と一致させながら上部比を変化させると、従来のドミナント風進行が作りやすい。累積比も意識するとより良いだろう。最低音を一致させるには再宣言と累積比1の二種類の方法がある。このような従来的なコード進行は汎純正律のうちの∞-limit的な機能である(比率主軸と対比して)。
100ms, prefreq=400
500ms, 1:1, 1200ms
500ms, 5:4, 1200ms
500ms, 3:2, 1200ms
1000ms, prefreq=400
2000ms, 1:1, 1200ms
2000ms, 4:3, 1200ms
2000ms, 5:3, 1200ms
3000ms, prefreq=400
3500ms, 1:1, 1200ms
3500ms, 3:2, 1200ms
3500ms, 9:8, 1200ms
4000ms, prefreq=400
5000ms, 1:1, 1200ms
5000ms, 5:4, 1200ms
5000ms, 3:2, 1200ms
Order-1での従来的なコード進行
100ms, prefreq=600
500ms, 1:1, 1200ms
500ms, 5:4, 1200ms
500ms, 3:2, 1200ms
1000ms, prefreq=600
2000ms, 1:1, 1200ms
2000ms, 5:4, 1200ms
2000ms, 3:2, 1200ms
2000ms, 11:8, 1200ms
3000ms, prefreq=600
3500ms, 1:1, 1200ms
3500ms, 5:4, 1200ms
3500ms, 9:13, 1200ms
4000ms, prefreq=600
5000ms, 1:1, 1200ms
5000ms, 5:3, 1200ms
5000ms, 3:2, 1200ms
高次テンションも利用した従来的なコード進行
なお、中低音域で 22:23 のような分子・分母が大きい近接比率を使用すると、構成音の周波数差が数 Hz 程度に収まることによる うなり が強く発生し、濁って聴こえる場合がある。特に意図的な効果を狙わない限り、低域では ±100 cent 以上離すかオクターブ処理するなどして回避した方が無難である。(ちなみにこの聴感的特徴は微分音コードあてゲームにも頻繁に利用できる。)
100ms, prefreq=200
200ms, 1:1, 4000ms
500ms, 23:22, 4000ms
うなり
4. まとめと今後の展望
4-1. 本稿の要点
1. 汎純正律の位置づけ
あらゆる有理数比を許容することで、従来の n-limit純正律 を包含しつつ無限次元の音程空間を開いた。比率列それ自体を作曲素材とみなす点が決定的な転換である。
2. 旋律の生成原理
絶対音高や調的中心を前提とせず、比率の列を操作することで反復・回文・連鎖など従来型の句読を再構成できる。周期総乗=1 のループやプリセット比率による部分律の抽出により、聴覚的な安定感も選択的に導入可能である。
3. 和声構造の分類
素因数階層によって Order-1/2/3 を定義したほか、シンプルなコード進行の記述例を提示した。
4-2. 課題
1.理論構築
従来の音楽とは異なる比率的アプローチによる経験則を集め、まとめるなどして作曲法を体系化する。
2.記譜法とビジュアライズ
効果的な記譜法や図式を考案・制作する。
4-3. 結語
っていう
0.おまけ
1000ms, 3:1, 1200ms
1300ms, 1:4, 1200ms
1600ms, 4:1, 1200ms
1900ms, 1:5, 1200ms
2200ms, 5:9, 1200ms
2500ms, 9:2, 1200ms
2800ms, 2:6, 1200ms
3100ms, 6:5, 1200ms
3400ms, 5:3, 1200ms
3700ms, 3:5, 1200ms
4000ms, 5:8, 1200ms
4300ms, 8:9, 1200ms
4600ms, 9:7, 1200ms
4900ms, 7:9, 1200ms
5200ms, 9:3, 1200ms
5500ms, 3:2, 1200ms
5800ms, 2:3, 1200ms
6100ms, 3:8, 1200ms
6400ms, 8:4, 1200ms
6700ms, 4:6, 1200ms
7000ms, 6:2, 1200ms
7300ms, 2:6, 1200ms
7600ms, 6:4, 1200ms
7900ms, 4:3, 1200ms
8200ms, 3:3, 1200ms
8500ms, 3:8, 1200ms
8800ms, 8:3, 1200ms
9100ms, 3:2, 1200ms
9400ms, 2:7, 1200ms
9700ms, 7:9, 1200ms
(以下省略)
円周率の格桁の比を周波数比にするやつの冒頭のフレーズ
⠀
